查看统计数据
除了「编码」页面展示的数据,本系统还提供了对方案的进一步统计分析功能,能够为方案作者提供更加深入的见解。这些统计分为两部分:「统计一」是元素序列表层面上的分析,不涉及到元素的具体安排;而「统计二」是码表层面上的分析,涉及元素的具体安排。
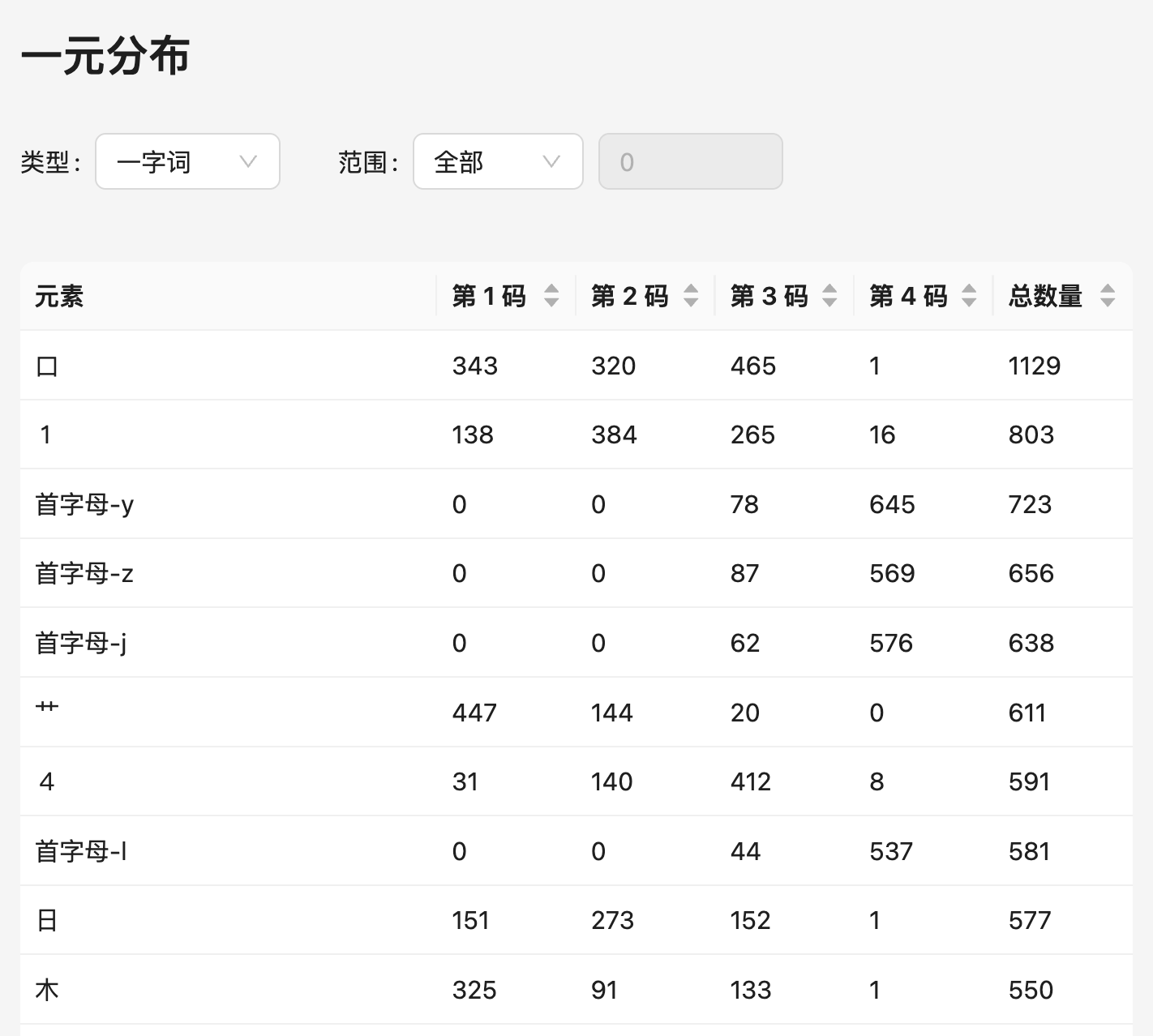
一元分布是指统计一个元素在方案的第一码、第二码、……直至最后一码上出现的次数、以及总次数的功能。
 该统计对于方案设计的意义在于:如果发现一个字根的使用频率过高,可以考虑改变拆分方式使得使用频率降低;反之,如果出现次数过少,则可以考虑删除此字根,以降低学习成本。
该统计对于方案设计的意义在于:如果发现一个字根的使用频率过高,可以考虑改变拆分方式使得使用频率降低;反之,如果出现次数过少,则可以考虑删除此字根,以降低学习成本。
在统计一元分布时,可以筛选统计的范围。当「类型」选取「一字词」时,只会统计一字词的元素序列中的出现次数,而选取「多字词」时只会统计多字词。而「范围」可以选取「全部」或按频率排序的「前 N 个」,例如可以统计「前 5000 字中用到的元素的数量多少」。
在介绍「统计一」的其余功能之前,我们首先引入一个概念:重码的阶数。
- 如果两个词的元素序列完全相同,那么无论如何这两个词都会发生重码。例如,在米十五笔中「另、叻」两个字的元素序列都是「口、力、首字母-l」。将这种情况称为「零阶重码」;
- 如果两个词的元素序列有一个不相同而其余都相同,那么当且仅当所不同的这一对元素的编码相同时会发生重码。例如,在米十五笔中「守、时」两个字的元素序列分别是「宀、寸、首字母-s」和「日、寸、首字母-s」,但因为「宀」和「日」都在
i键上,使得两个字发生重码。 - 以此类推,如果两个词的元素序列有 N 个不相同而其余都相同,那么当且仅当所有 N 对元素的编码都各自相同时会发生重码。
这种分类揭示了重码的内在结构,对方案的设计是有益的。例如,即使是对于乱序方案来说,如果有大量的零阶重码存在,其乱序优化也不可能将重码降低到很低的水平。
多元分布是对一元分布的进一步推广,它不仅能回答诸如「第一码出现某元素的数量有多少」,还能回答诸如「同时满足第一码出现元素 x、第二码出现元素 y 的数量有多少」,乃至更多条件同时成立的问题。
多元分布与重码阶数密切相关。例如,对一个最长码长为四的方案统计四元分布(即统计第一至第四码分别是某些元素),就等价于去寻找它的零阶重码。例如,下图中展示了满足第一到第四码的元素分别是「立、𠂇、十、首字母-b」的汉字有「瓣、辨、辩、辫」这四个,则说明这四个是零阶重码。系统会计算出零阶重码的数量。
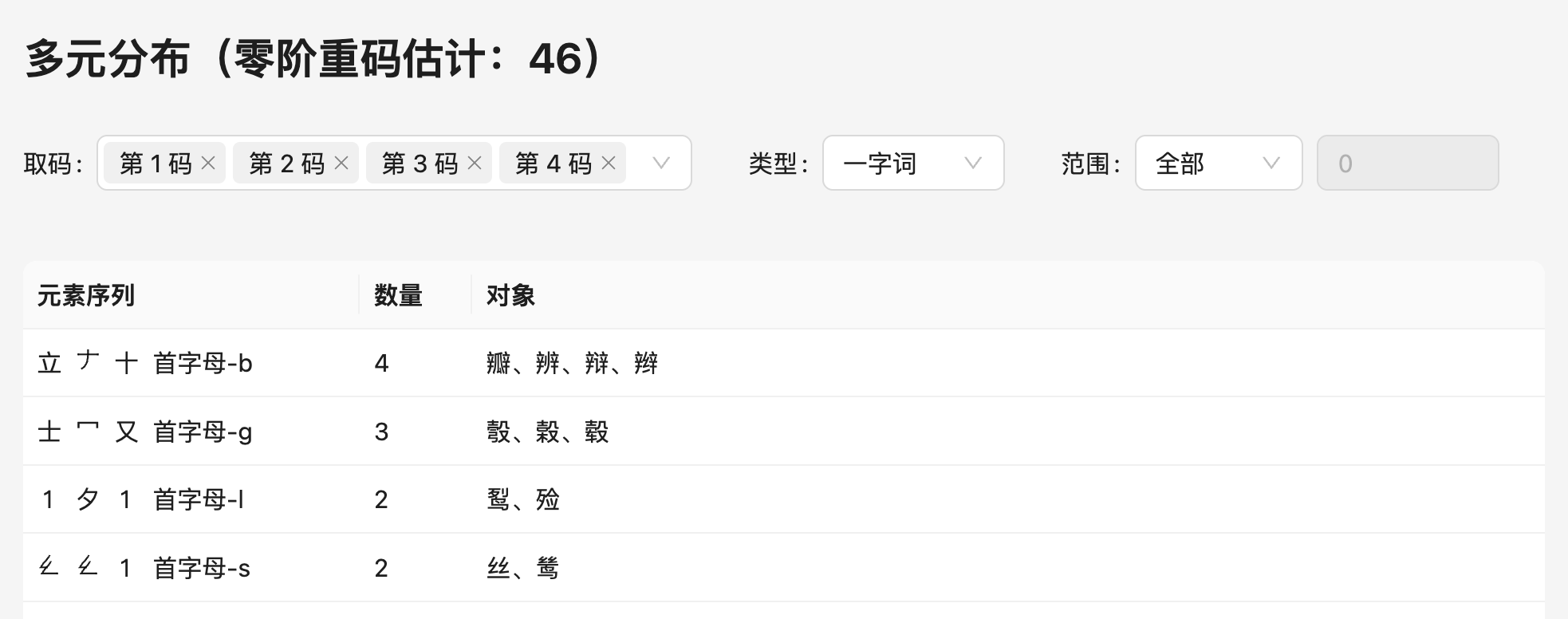
如果四元分布揭示了零阶重码的信息,那么三元分布又揭示了怎样的信息呢?在这个示例中,我们可以将「取码」一栏中取消「第 1 码」,只考虑第 2 ~ 4 码的分布情况,可以发现:
 有 19 个字都满足第二码到第四码分别是「全字头、龴、首字母-l」。这说明如果这 19 个字中某些字的第一个元素如果和另一个字的第一个元素位于同一个键上,就会发生重码。一种极端的情况是,如果对于一个 26 键方案,其三元分布的某一项大于等于 27,则一定会发生重码(抽屉原理)。因此,三元分布揭示了关于一阶重码的信息。不过,对于一阶重码来说在不考虑元素布局的情况下不能精确计算,因此在这里展示的一阶重码是个估计值。
有 19 个字都满足第二码到第四码分别是「全字头、龴、首字母-l」。这说明如果这 19 个字中某些字的第一个元素如果和另一个字的第一个元素位于同一个键上,就会发生重码。一种极端的情况是,如果对于一个 26 键方案,其三元分布的某一项大于等于 27,则一定会发生重码(抽屉原理)。因此,三元分布揭示了关于一阶重码的信息。不过,对于一阶重码来说在不考虑元素布局的情况下不能精确计算,因此在这里展示的一阶重码是个估计值。
与一元分布一样,多元分布计算时也可以根据一字词/多字词、词频筛选。
边际一阶重码计算
Section titled “边际一阶重码计算”边际一阶重码的含义为:假定某几个元素位于同一个键上,导致必然出现的一阶重码。例如,在米十五笔中,查看「宀」和「日」合并导致的重码,结果如图所示:

边际一阶重码可以一次性合并两个字根也可以合并更多个字根。您可以点击「+」「−」增加或减少合并字根的数量。
与多元分布一样,边际一阶重码计算时也可以根据一字词/多字词、词频筛选,以及确定考虑哪些码位。
统计二是在码表层面上的分析。
一元分布和二元分布
Section titled “一元分布和二元分布”这里一元分布的含义是统计编码中各个字符的出现频率。根据需要,可以选择统计的维度是哪些码;选择统计的对象是一字全码、一字简码、多字全码、多字简码;选择是否按词频加权。类似地,二元分布是统计任意两个码上各字符出现频率构成的矩阵。

在指法二维分布表格中,矩阵的纵、横坐标分别是第一码和第二码,区块上的颜色表示当前组合的当量数值,而数字表示当前组合的数量。您也可以开启「加权」切换为计算组合频率。

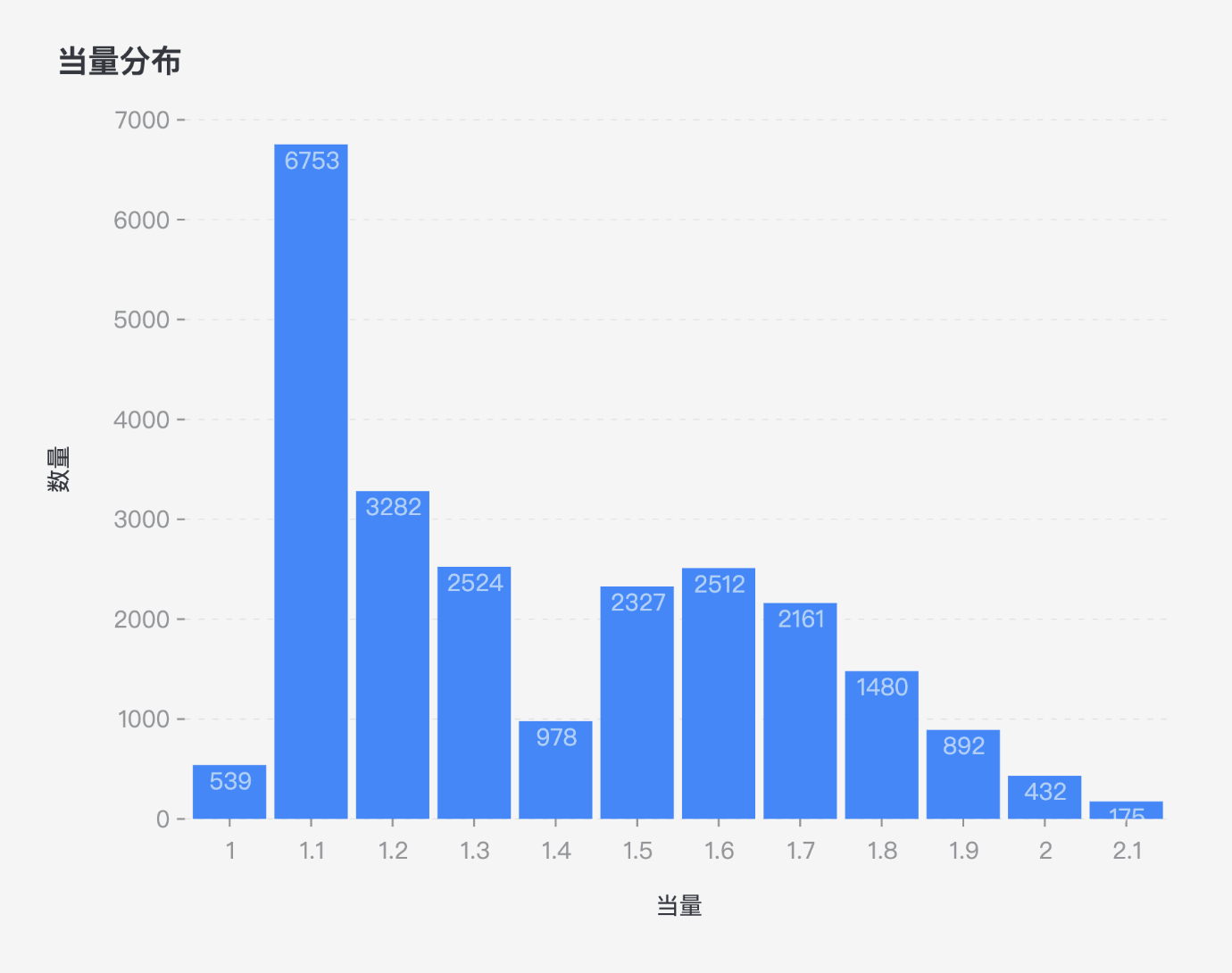
在当量分布图中,横轴是当量数值,而纵轴是位于这个数值上的组合数量。
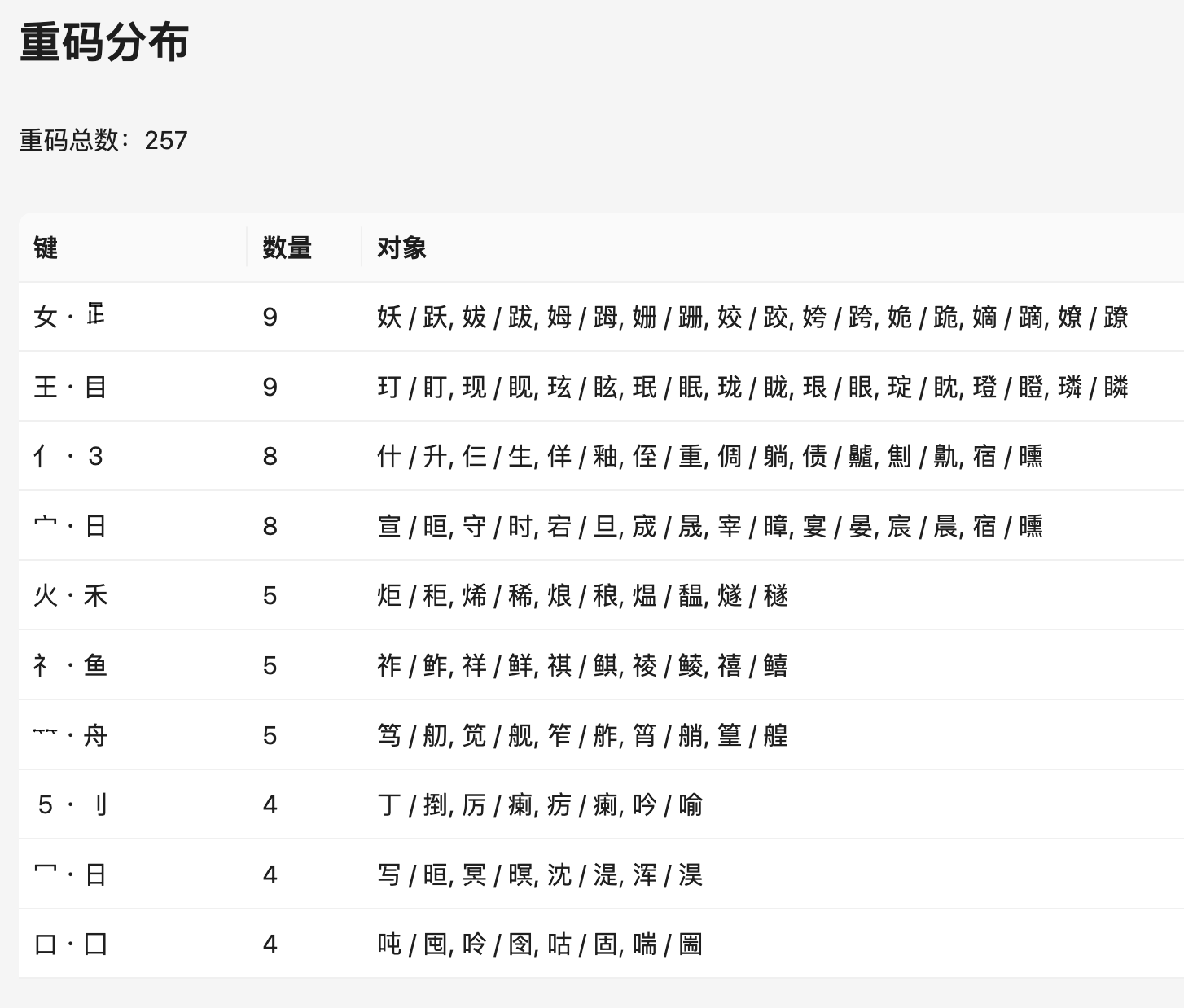
重码分布计算了在所有的全码重码当中,由哪些元素导致的冲突比较多。本模块目前不能根据一字词/多字词/全简码/频率筛选,有待提升。